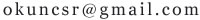如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长
来自: 更新日期:早些时候
如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长~
∵AB=AD,∠ABG=∠D=90°
∴△ABG≌△ADF
∴∠BAG=∠DAF,AF=AG
∵∠EAF=45°
∴∠GAE=∠BAG+∠BAE
=∠DAF+∠BAE
=45°
∴△GAE与△FAE中
∠GAE=∠EAF,
AG=AF,
AE=AE
∴△GAE≌△FAE
∴EF=GE=BG+BE
=DF+BE
∴△CEF的周长=CE+CF+EF
=CE+CF+DF+BE
=BC+CD
=2a
如果满意记得采纳哦!
你的好评是我前进的动力。
(*^__^*) 嘻嘻……
我在沙漠中喝着可口可乐,唱着卡拉ok,骑着狮子赶着蚂蚁,手中拿着键盘为你答题!!!
设be为m,三角形abe和三角形ecf相似,所以m比上cf等于ab比ec.就能解了
如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长视频
相关评论:15118345485:如图,正方形ABCD的边长为6cm,E,F分别是AD,BC的中点M,N,K分别是AB,CD...
鄂琼侄S△DEP+S△BFP=1\/2*1\/2边长*边长=1\/4*6*6=9(cm^2)S△KCP+S△MNP=1\/2*1\/3边长*边长=1\/6*6*6=6(cm^2)S阴影=S△DEP+S△BFP+S△KCP+S△MNP=9+6=15(cm^2)
15118345485:如图,正方形ABCD的边长为2,三角形ABE是等边三角形。求角ACE的度数和求...
鄂琼侄等边三角形ABE 则 AB=EB=BC 则三角形EBC是等腰三角形 且 ∠ABC=90 ∠EBA=60 则 ∠EBC=150 则 ∠BCE=∠CEB=15 △AGB与△BGC 中 AB=BC BG=BG ∠ABG=∠GBC 则 △AGB≌△BGC 则∠BAG=∠BCG=15 ∠AGB=∠CGB 则∠AGD=∠CGD 三角形AEG中 ∠AEG=∠AEB...
15118345485:如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.则...
鄂琼侄5 设BE=x,则EC=4﹣x,先利用等角的余角相等得到∠BAE=∠FEC,则可判断Rt△ABE∽Rt△ECF,利用相似比可表示出FC= ,则DF=4﹣FC=4﹣ = x 2 ﹣x+4= (x﹣2) 2 +3,所以x=2时,DF有最小值3,而AF 2 =AD 2 +DF 2 ,即DF最小时,AF最小,AF的最小值为 =5.解...
15118345485:如图,正方形ABCD的边长为4cm,两动点P、Q分别同时从D、A出发,以1cm\/秒...
鄂琼侄∵正方形APOQ,∴AP=PO=AQ,∴4-x=x,解得:x=2.故当P、Q出发后2秒时,四边形APOQ为正方形;(2)∵四边形ABCD是正方形 ,∴DO=OA,∠PDO=∠OAB=45°,又∵PD=AQ,∴△AQO≌△DPO(SAS),∴S△AQO=S△DPO,设P、Q出发后a秒时,S△PQO= 5 32 S正方形ABCD,∴AP=4-a,...
15118345485:如图,正方形ABCD的边长为1㎝,M,N分别是BC,CD上两个动点,且始终保持AM...
鄂琼侄在△ABM中,有∠BAM+∠B=∠AMC=∠AMN+∠CMN 由AM⊥MN得∠AMN=∠B=90° 所以∠BAM=∠CMN,加上∠B=∠C=90° 有△ABM∽△MCN,得AM\/MN=AB\/MC 由已知△ABM∽△AMN得AB\/AM=BM\/MN,即AM\/MN=AB\/BM 所以AB\/MC=AB\/BM,得BM=MC 则M是BC中点,有x=BM=BC\/2=1\/2(cm)所以当x=1\/...
15118345485:如图,正方形abcd的边长为4厘米,AE=2BE,求三角形CDF的面积?
鄂琼侄所以:AE=8\/3 BE=4\/3 又: △AEF∽△DFC 所以:h:(4-h)=DC:AE=3:2 则:h=2.4 S△DFC=4×2.4÷2=4.8 CM²或者:∵AE\/BE=2 AE\/(AE+BE)=2\/3 AE\/AB=2\/3 AE\/CD=2\/3 ∴AE\/CD=AF\/FC=2\/3 ∵S△ACD=1\/2S正方形ABCD=1\/2×4²=8 △ADF...
15118345485:如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF垂直...
鄂琼侄∴△PFA∼△ABE 2解:如果令△PFE∼△ABE 那么△PFE∼△PFA 因为PF⊥AE ∴∠EPF=∠APF或∠EPF=∠PAF 若∠EPF=∠APF △EPF≅△APF 则P点在P1位置 此时AF1=EF1 由勾股定理AE=2√(5)AF1=√(5)∴P1F1=2√(5)∴X=AP1=5 若∠EPF=∠PAF P在P2位置为AD中点 X=...
15118345485:如图,正方形ABCD的边长为10厘米,CF=2BF,AE=3BE,那么阴影部分的面积为...
鄂琼侄解:设AF和DE交于G,∵S△EGF\/S△DGF=EG\/DG(因为同高),S△EGA\/S△DGA=EG\/DG,∴(S△EGF+S△EGA)\/(S△DGF+S△DGA)=EG\/DG,即S△AEF\/S△AFD=EG\/DG,S△AEF=15\/2×10\/3÷2=25\/2,S△AFD=10×10÷2=50,EG\/DG=(25\/2)\/50=1\/4,S△ADE=15\/2×10÷2=75\/2,S...
15118345485:如图,正方形ABCD的边长为1,AC是对角线,AE平分角BAC,EF⊥AC于点F(1...
鄂琼侄1、∠BAE=∠FAE,∠B=∠AFE=90°,AE=AE 所以△ABE全等于△AFE 所以BE=EF 在Rt△EFC中,∠FCE=π\/4 所以Rt△EFC是等腰直角三角形 所以EF=FC ∴BE=CF 2、设BE=a,则CF=a △ABE全等于△AFE ∴AF=AB=1 ∴AF+CF=1+a=AC=根号2 所以a=根号2 -1 即BE=根号2 -1 ...
15118345485:如图,正方形ABCD的边长为4,点E、F分别在边BC、CD上,且CF=1。若∠AFE...
鄂琼侄这个题目可以用相似三角形来解,简单方便。由于是正方形,∠D=∠ECF=90°,且∠AFE=90° 得出∠DAF=∠EFC 所以△ECF与△FDA为相似三角形,即CE:FD=CF:DA 那么CE=3\/4
解:∵四边形ABCD为正方形,∴AB=AD,∠BAD=∠B=90°,∴把△ADF绕点A顺时针旋转90°可得到△ABG,如图,∴AG=AF,BG=DF,∠GAF=90°,∠ABG=∠B=90°,∴点G在CB的延长线上,∵∠EAF=45°,∴∠EAG=∠GAF-∠EAF=45°,∴∠EAG=∠EAF,在△EAG和△EAF中,AE=AE∠EAG=∠EAFAG=AF,∴△EAG≌△EAF(SAS),∴EG=EF,而EG=BE+BG=BE+DF,∴EF=BE+DF,∴△CEF的周长=CE+CF+BE+DF=CB+CD=a+a=2a.
解:如图,延长CB至G,使BG=DF
∵AB=AD,∠ABG=∠D=90°
∴△ABG≌△ADF
∴∠BAG=∠DAF,AF=AG
∵∠EAF=45°
∴∠GAE=∠BAG+∠BAE
=∠DAF+∠BAE
=45°
∴△GAE与△FAE中
∠GAE=∠EAF,
AG=AF,
AE=AE
∴△GAE≌△FAE
∴EF=GE=BG+BE
=DF+BE
∴△CEF的周长=CE+CF+EF
=CE+CF+DF+BE
=BC+CD
=2a
∵AB=AD,∠ABG=∠D=90°
∴△ABG≌△ADF
∴∠BAG=∠DAF,AF=AG
∵∠EAF=45°
∴∠GAE=∠BAG+∠BAE
=∠DAF+∠BAE
=45°
∴△GAE与△FAE中
∠GAE=∠EAF,
AG=AF,
AE=AE
∴△GAE≌△FAE
∴EF=GE=BG+BE
=DF+BE
∴△CEF的周长=CE+CF+EF
=CE+CF+DF+BE
=BC+CD
=2a
如果满意记得采纳哦!
你的好评是我前进的动力。
(*^__^*) 嘻嘻……
我在沙漠中喝着可口可乐,唱着卡拉ok,骑着狮子赶着蚂蚁,手中拿着键盘为你答题!!!
设be为m,三角形abe和三角形ecf相似,所以m比上cf等于ab比ec.就能解了
好的
.....
如图,正方形ABCD的边长为a,点E、F分别在边BC、CD上,且∠EAF=45°,求△CEF的周长视频
相关评论:
鄂琼侄S△DEP+S△BFP=1\/2*1\/2边长*边长=1\/4*6*6=9(cm^2)S△KCP+S△MNP=1\/2*1\/3边长*边长=1\/6*6*6=6(cm^2)S阴影=S△DEP+S△BFP+S△KCP+S△MNP=9+6=15(cm^2)
鄂琼侄等边三角形ABE 则 AB=EB=BC 则三角形EBC是等腰三角形 且 ∠ABC=90 ∠EBA=60 则 ∠EBC=150 则 ∠BCE=∠CEB=15 △AGB与△BGC 中 AB=BC BG=BG ∠ABG=∠GBC 则 △AGB≌△BGC 则∠BAG=∠BCG=15 ∠AGB=∠CGB 则∠AGD=∠CGD 三角形AEG中 ∠AEG=∠AEB...
鄂琼侄5 设BE=x,则EC=4﹣x,先利用等角的余角相等得到∠BAE=∠FEC,则可判断Rt△ABE∽Rt△ECF,利用相似比可表示出FC= ,则DF=4﹣FC=4﹣ = x 2 ﹣x+4= (x﹣2) 2 +3,所以x=2时,DF有最小值3,而AF 2 =AD 2 +DF 2 ,即DF最小时,AF最小,AF的最小值为 =5.解...
鄂琼侄∵正方形APOQ,∴AP=PO=AQ,∴4-x=x,解得:x=2.故当P、Q出发后2秒时,四边形APOQ为正方形;(2)∵四边形ABCD是正方形 ,∴DO=OA,∠PDO=∠OAB=45°,又∵PD=AQ,∴△AQO≌△DPO(SAS),∴S△AQO=S△DPO,设P、Q出发后a秒时,S△PQO= 5 32 S正方形ABCD,∴AP=4-a,...
鄂琼侄在△ABM中,有∠BAM+∠B=∠AMC=∠AMN+∠CMN 由AM⊥MN得∠AMN=∠B=90° 所以∠BAM=∠CMN,加上∠B=∠C=90° 有△ABM∽△MCN,得AM\/MN=AB\/MC 由已知△ABM∽△AMN得AB\/AM=BM\/MN,即AM\/MN=AB\/BM 所以AB\/MC=AB\/BM,得BM=MC 则M是BC中点,有x=BM=BC\/2=1\/2(cm)所以当x=1\/...
鄂琼侄所以:AE=8\/3 BE=4\/3 又: △AEF∽△DFC 所以:h:(4-h)=DC:AE=3:2 则:h=2.4 S△DFC=4×2.4÷2=4.8 CM²或者:∵AE\/BE=2 AE\/(AE+BE)=2\/3 AE\/AB=2\/3 AE\/CD=2\/3 ∴AE\/CD=AF\/FC=2\/3 ∵S△ACD=1\/2S正方形ABCD=1\/2×4²=8 △ADF...
鄂琼侄∴△PFA∼△ABE 2解:如果令△PFE∼△ABE 那么△PFE∼△PFA 因为PF⊥AE ∴∠EPF=∠APF或∠EPF=∠PAF 若∠EPF=∠APF △EPF≅△APF 则P点在P1位置 此时AF1=EF1 由勾股定理AE=2√(5)AF1=√(5)∴P1F1=2√(5)∴X=AP1=5 若∠EPF=∠PAF P在P2位置为AD中点 X=...
鄂琼侄解:设AF和DE交于G,∵S△EGF\/S△DGF=EG\/DG(因为同高),S△EGA\/S△DGA=EG\/DG,∴(S△EGF+S△EGA)\/(S△DGF+S△DGA)=EG\/DG,即S△AEF\/S△AFD=EG\/DG,S△AEF=15\/2×10\/3÷2=25\/2,S△AFD=10×10÷2=50,EG\/DG=(25\/2)\/50=1\/4,S△ADE=15\/2×10÷2=75\/2,S...
鄂琼侄1、∠BAE=∠FAE,∠B=∠AFE=90°,AE=AE 所以△ABE全等于△AFE 所以BE=EF 在Rt△EFC中,∠FCE=π\/4 所以Rt△EFC是等腰直角三角形 所以EF=FC ∴BE=CF 2、设BE=a,则CF=a △ABE全等于△AFE ∴AF=AB=1 ∴AF+CF=1+a=AC=根号2 所以a=根号2 -1 即BE=根号2 -1 ...
鄂琼侄这个题目可以用相似三角形来解,简单方便。由于是正方形,∠D=∠ECF=90°,且∠AFE=90° 得出∠DAF=∠EFC 所以△ECF与△FDA为相似三角形,即CE:FD=CF:DA 那么CE=3\/4